作者:林晋宇

在这个信息爆炸的社会,想要从海量的新闻中筛选出真实有效的信息并非易事。本篇文章将为大家科普一个广泛存在的奇特现象——辛普森效应。
一、为什么平均消费下降,但每个分组的组内平均消费却增高?
简单假设一个情况:城市A,人口100万人,市民的收入划分为图1所示的三个档次:
收入在0-20万(低收入)之间的约74万人,假设收入均值为12.79万元;收入在20-50万(中收入)之间的约22万人,假设收入均值28万元;收入在50万以上(高收入)的有4万人,假设收入均值287万元,每个收入区间内的人收入按照其均值幂律分布,我们用python生成随机数模拟上述过程。
图1:初始情况下平均收入分布

当经济不景气之时,假设每个人的收入都减少了10%,那么每个档位的平均收入将发生什么变化呢?
先说答案,每一个档位的人均收入都会提高。总体人群收入确实是下降了,但是在分别统计的时候,却会出现完全背离的结果。这真的合理吗?
图2:经济不景气下平均收入分布
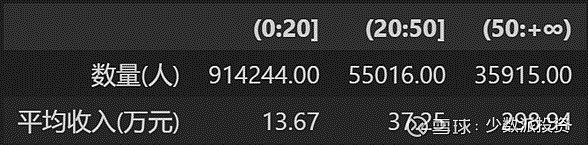
其实细心的朋友已经看到每个统计区间内的人数有较大的变动,而原因也正来源于此。首先我们看高收入档位人群变化,会发现原先有42873人,收入减少10%后,人数变成了35915人。接近7000人原本收入在50-55万之间,收入下降10%后收入变成了45-50万,因为不满足50万的分界而被分流到20-50万的中收入区间。高收入档位由于分流出去一批人导致平均收入反而上升了。另外两个档位原本的平均收入虽然也减少,但由于得到上一档位的人员补充,平均收入却也是上升的。最终形成了诡异的三赢局面。
二、辛普森效应和幂律分布
这一现象于20世纪初就有人讨论。直到1951年才被英国统计学家辛普森解释,后来就以他的名字命名此悖论即辛普森悖论。辛普森悖论描述了一种现象:有时候,两组数据各自都满足某种性质,可是当你把这两组数据合并起来考虑时,却会得到相反的结论。
这个模拟实验的现象也确实曾发生在经济衰退的日本身上。值得一提的是,实验中人群收入分布服从的是长尾分布,也就是遵守了人们口中常说的二八定律,20%的人获得了80%的财富。
图3:幂律分布
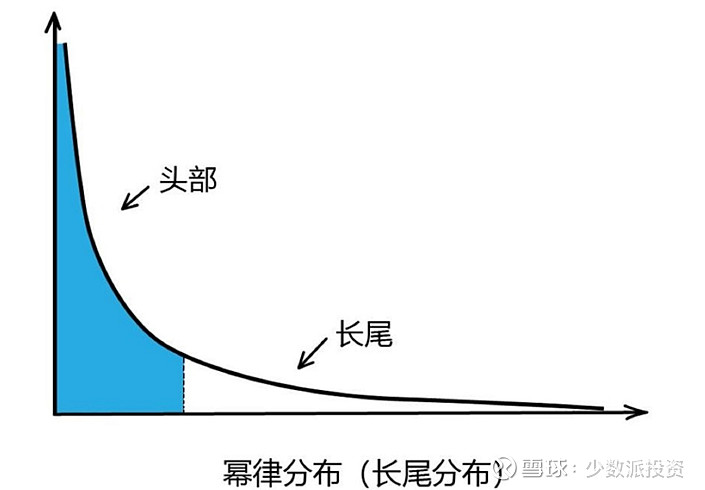
图3里横坐标代表随机变量的取值,纵坐标代表发生的概率。幂律分布就是一条向下的曲线,拖着一个长长的尾巴,它的含义就是它的数据波动非常地大,少数点的数值特别高,大多数的点数值都很低,最大和最小的点之间,可能相差好几个数量级。
幂律分布有个好玩的数学特征,就是无标度,也叫“无尺度”,意思是在任何观测尺度下,都呈现同样的分布特征。比如,图书销量是服从幂律分布的,最畅销那本书的销量在前10名销量中占的比例,和前10名的销量在前100名的销量中占的比例,和前100名在前1000名的总销量中占的比例,大体都是相同的。基于这个特征,幂律分布下随机变量波动的范围非常大,常用的平均值、标准差在这里都失去了意义。这时统计城镇居民收入的时候平均数完全没有意义,比如我和马云一平均我也是超级富豪了,这完全没有任何意义。
辛普森悖论的重要性在于它揭示了我们看到的数据并非事实全貌。例如我们经常能看到朋友圈转发的一些养生文章,什么《惊人发现:吸烟有助于长寿》、《喝牛奶比喝豆浆好100倍》、《多吃菠菜可以美白》等。
你会发现,这类包含着大量实验数据、结论却与人们普遍认知截然相反的文章并没有使用假数据,作者只是“巧妙”地通过各种限定条件、筛选角度来暗示读者如何思考,并让读者接受其观点来达到自己的传播目的。正如上面城市A平均收入的例子,如果不谈整体平均收入下滑,不谈各收入区间人数变化,只讲统计下来每个区间平均收入增加并给出权威可靠的数据来源,我们会不会被影响而真的认为居民收入确实提高了呢?
数据是客观的,真实的,但是不同的人利用同样的数据,可以讲出不同的故事。所以我们经常看到上市公司发布的财务信息避重就轻,挑更有利于自己的数据公布,而表现不好的财务数据经常选择性的回避。
《简单统计学》里写道:混杂因素常常出现在使用观测性数据的研究中,因为人们无法通过现实的方法使这些因素维持恒定。所以,我们应该牢记:一项研究的结论有可能受到混杂因素的干扰。
再举几个有趣的例子:
1.阿拉斯加航空公司在五个存在竞争的主要机场,拥有优于另一家航空公司的准点运行记录,但其总体准点记录则不如竞争对手,为什么?
因为阿拉斯加航空拥有许多飞往西雅图的航班,而西雅图的天气问题经常导致飞机延误 。
2. 2021年8月,根据英格兰公共卫生局(PHE)最近发布的一份报告,接种疫苗后死于新冠的人比未接种疫苗的人多,国外有网友在Facebook发文得出疫苗充分地增加了感染者的住院死亡风险。这是真的吗?
事实上,Facebook文章对接种人群分析有误,英国的疫苗接种策略是首先为年龄较大、较脆弱的人接种疫苗,其死亡率天然就更高,计算比例时忽略了数据的年龄组别,仅使用不分年龄的全体数字,令其得出与数据不符的结论。
3.假设你有一个朋友需要实施脑部手术,有两位医生可供选择,其中A医生收治的100个病人当中90人存活,而B医生收治的100个人中80人存活。是不是A医生就比B医生好呢?
其实并不一定,进一步了解之后,发现A医生收治了10个重症患者,存活率为30%,90个轻症患者存活率为96.7%。而B医生收治了40个重症患者存活率为52.5%,60个轻症患者存活率为98.3%。在区分了重症和轻症后,不管怎么看,更好的选择都是B医生。
4.美国加州大学伯克利分校在1973年因为男女研究生录取比例的的问题陷入一场舆论风波。那年伯克利公布研究生招生名单时,有人发现男生的录取率为44%,而女生的录取率却仅为35%,男生的录取率比女生高了四分之一。如此“明目张胆的性别歧视行为”引起了众多女同学的强烈抗议,要求伯克利给一个说法。迫于压力,伯克利大学不得不针对这一招生事件展开调查,但是调查结果却令人大跌眼镜:伯克利许多学院招收学生时,明明是女生的录取率更高。
我们挑其中一组数据来进行解释,申请A专业的825名男生录取率是62%,108名女生录取率是82%;申请B专业的320名男生录取率是22%,524名女生录取率是41%,两者都是女生录取率更高。但由于更多的女生报了录取率更低的B专业,因此造成了总体统计下来女生录取率更低。
三、如何避免辛普森效应?
想要完全避免辛普森悖论的影响并不容易。理论上,潜在变量是无穷无尽的,一些别有用心之人总是能够操纵数据得到对自己有利的结果。
一般而言,“辛普森悖论”的产生有两个条件:
第一,分组数据结构不一样。以上面伯克利学院的录取为例,A专业在男女生中的录取率分别是62%和82%,远高于B专业22%、41%的录取率;不同的数据组之间成功率有明显差异。
第二,作比较的两者在分组数据中的比例分配有所差别。申请伯克利的男生虽然在两个专业的录取比例都低于女生,但是大部分男生都申请了成功率较高的A专业,而女生更多的选择了成功率更低的B专业,所以整体来讲,男同学通过的比例反而会高一些。
遇到这两个特征我们就要小心是否数据中存在辛普森效应了,进一步思考下整个数据生成的过程,考虑因果模型,凡事多问几个“为什么”。这个数据是怎么得来的?哪些因素影响着目前的结果?哪些因素是明摆着的,哪些又是被隐藏起来却至关重要的?数据中是够蕴藏着作者的某种主观意图?
辛普森悖论让我们清晰地认识到,要对数字本身持怀疑态度,只有理性思考、挖掘更深层次的东西、多角度的综合评判,才能揭示事实全貌、不断接近真相。