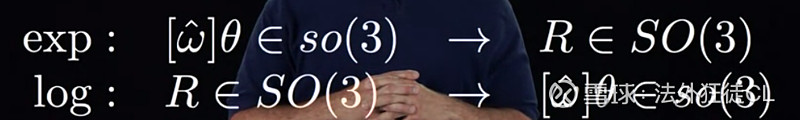3.1 Introduction to Rigid-Body Motions
1)三维直角坐标系,用右手准则:
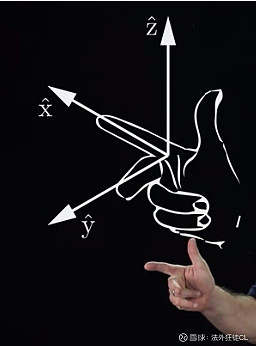
2)右手准则:右手手指卷曲的方向决定正向旋转的方向

3)frame of refercence 是参考坐标系,一个新的metrics的三个向量分别通过和参考坐标系作对比得出,并且都是竖向量,然后组合在一起。可以用Rsb表示,s-frame of reference,b-被表示向量或者metrics,很多时候sb可以省略。
4 )special orthogonal group SO(3)是3*3的矩阵,满足
a、Rt*R=I ,I-identiy metrics-对角线全是1的矩阵

b、det R=1(det 矩阵的行列式,eg. ad-bc)
5)SO(3)的定义:Special Orthogonal Group SO(3) 是用于描述三维空间中旋转的矩阵集合,其中的每个矩阵都对应于一个唯一的三维旋转。 SO(3) 中的元素是特殊正交矩阵,通常被称为旋转矩阵,它们用于表示物体在三维空间中的旋转操作。这些矩阵具有特定的性质,对于许多应用领域非常重要。
6)旋转矩阵的性质

3.2.1 旋转矩阵
1)旋转矩阵的三个用处
a、表示一个物体的方向或者姿态
b、更改参考坐标系:Rsc=RsbRbc,P(向量)s=RsbP(向量)b结果上可以当做是约掉了b
c、旋转一个向量或者坐标系:
Rsb=R=Rot(z head,90度)
p‘s=Rps,就把p在原有坐标系里从以z为轴旋转了90度
Rsc‘=RRsc,Rsc‘’=RscR,R的位置不一样,得到的结果不一样,在右侧执行操作意味着操作是基于第二个下标的坐标系c 完成的
注意,矩阵的一些性质:Rbc的逆矩阵=Rcb
2)旋转矩阵B的角速度:R-dot
注意:SO(3) 之所以被认为是一个曲面,是因为它涉及到描述三维空间中连续旋转的各种参数,而这些参数构成了一个连续的曲线或曲面。
3.2.2 角速度
1)旋转矩阵有9个元素,x,y,z轴各自的三维坐标,角速度,R-点,用3个元素表示
2)在任何给定的方向上,角速度的空间是一个与该方向相切的平坦的三维向量空间。"相切的平坦的三维向量空间" 意味着在某一方向上的角速度可以被表示为一个普通的三维向量,而不需要考虑弯曲或复杂的数学结构。
3)公式:计算旋转矩阵的角速度,R-点(s是 space frame,b是body frame,其实计算的是Rsb-点,但通常把下标sb省略)
a、omega s=theta-dot*omega-hat_s
theta-dot:旋转速度
omega-hat_s:以s为参考坐标系,单位长度的向量
omega s:角速度向量
b、[omega_s]:b frame中三个轴的角速度:用 [ ]表示一个矩阵,这是个3*3个元素的矩阵。
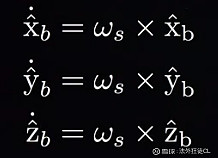
注意:这些个3x3 反对称矩阵(3 by 3 skew-symmetric matrices)是一种特殊类型的矩阵,它们满足以下条件:矩阵的转置等于它的负矩阵,即 A^T = -A,其中 A 表示这个矩阵。 这些矩阵具有一些特定的数学性质,其中包括它们的主对角线元素都是零,而非对角线元素关于主对角线对称,因此总共有3个自由度。so(3)是 SO(3) 的一个代数表示,与 SO(3) 相比(9个自由度),它的维度更低。
c、R-dot=[omega_s]*R
4)omega s(=theta-dot*omega-hat_s)又称为指数坐标。"指数坐标"是一种可替代旋转矩阵的方式。旋转矩阵通常是一个3x3的矩阵,用于描述一个坐标系相对于另一个坐标系的旋转。"指数坐标"提供了另一种方法来表示同样的旋转信息,但它是基于参数化的,通常包括三个参数。
5)矩阵指数
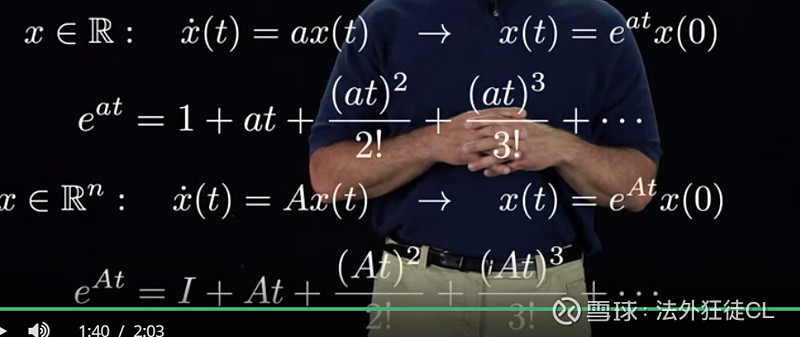
6)Rodrigues' formula:提供了一种将旋转表示为角度和轴向量的方式。它非常有用,因为它使得旋转的表示更加紧凑,并且可以轻松地进行旋转矩阵到轴角表示或轴角表示到旋转矩阵的转换。
这里的omega head,我觉得应该是角速度向量
theta,是旋转的角度

7)旋转矩阵和‘角度和轴向量’的关系