人脑大约由10^12个神经元组成,而其中的每个神经元又与约10^2~10^4个其他神经元相连接,如此构成一个庞大而复杂的神经元网络。
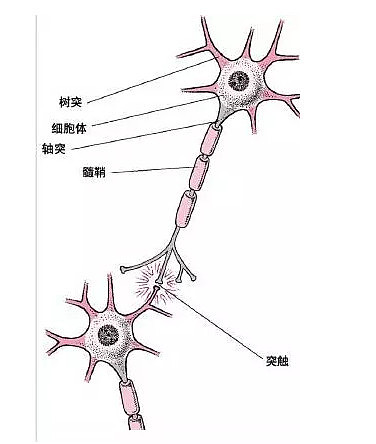
神经元是大脑处理信息的基本单元,它是以细胞体为主体,由许多向周围延伸的不规则树枝状纤维构成的神经细胞,其形状很像一棵枯树的枝干。它主要由细胞体、树突、轴突和突触(Synapse,又称神经键)组成。
神经元细胞的特点:
1.树突、轴突、突触分别相当于细胞体的输入端、输出端及输入/输出接口(I/O),并且多输入单输出;
2.兴奋型和抑制型突触决定神经细胞兴奋和抑制(分别对应输出脉冲串频率高低),其中脉冲串代表神经元的信息;
3. 细胞体膜内外电位差(由突触输入信号总和)的升高超过阈值产生脉冲,神经细胞进入兴奋状态;
4. 突触延迟使输入与输出间有固定时滞。

1943年,基于生物神经网络的麦卡洛克-皮茨神经元模型(McCulloch-Pitts′ neuron model)诞生。它由心理学家Warren McCulloch和数学家Walter Pitts合作提出。
McCulloch-Pitts模型的基本思想是抽象和简化生物神经元的特征性成分。这个模型不需要捕捉神经元的所有属性和行为,但要足以捕获它执行计算的方式。McCulloch-Pitts模型的6个特点中前面4点和之前总结的生物神经元一致,具体对应如下:
1.每个神经元都是一个多输入单输出的信息处理单元;
2.神经元输入分兴奋性输入和抑制性输入两种类型;
3.神经元具有空间整合特性和阈值特性;
4.神经元输入与输出间有固定的时滞,主要取决于突触延搁;
5.忽略时间整合作用和不应期;
6.神经元本身是非时变的,即其突触时延和突触强度均为常数。
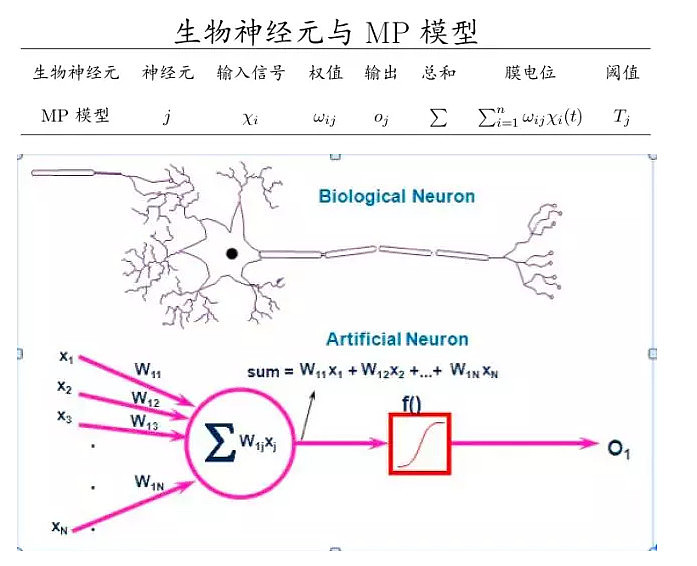
McCulloch-Pitts模型公式如下:
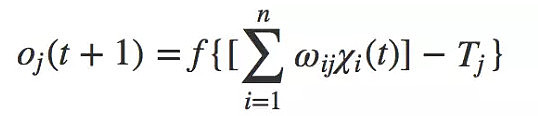
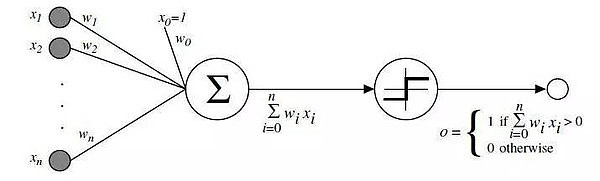
xi(i=1,2,…,n)为加于输入端(突触)上的输入信号,oj为输出信号;ωij为相应的突触连接权重系数,它是模拟突触传递强度的一个比例系数,∑表示突触后信号的空间累加;Tj表示神经元的阈值,f表示神经元的响应函数。响应函数的基本作用:1、控制输入对输出的激活作用;2、对输入、输出进行函数转换;3、将可能无限域的输入变换成指定的有限范围内的输出。
其运作规则是:时间离散,时刻t(t=0,1,2,……)得到兴奋型输入xi,如果膜电位等于或大于阈值以及抑制型输入为0,则在时刻t+1,神经元细胞输出为1否则为0。

但是McCulloch-Pitts模型缺乏一个对人工智能而言至关重要的学习机制。1949年加拿大心理学家唐纳德·赫布(Donald Hebb)在出版的《行为的组织》一书中提出了其神经心理学理论,他认为知识和学习发生在大脑主要是通过神经元间突触的形成与变化,这个出人意料并影响深远的想法简称“赫布法则”:
当细胞A的轴突足以接近以激发细胞B,并反复持续地对细胞B放电,一些生长过程或代谢变化将发生在某一个或这两个细胞内,以致A作为对B放电的细胞中的一个效率增加。
通俗来讲就是两个神经细胞交流越多,它们连接的效率就越高,反之就越低。
在美国康奈尔大学航天实验室工作的心理学家弗兰克·罗森布拉特(Frank Rosenblatt)受到赫布基础性工作的启发,于1957年提出了"感知器" (Perceptron)模型。这是第一个用算法来精确定义神经网络的,感知器由两层神经元组成,输入层接收外界信号,输出层是McCulloch-Pitts神经元,即阈值逻辑单元,也称为神经网络的一个处理单元( PE,Processing Element )。
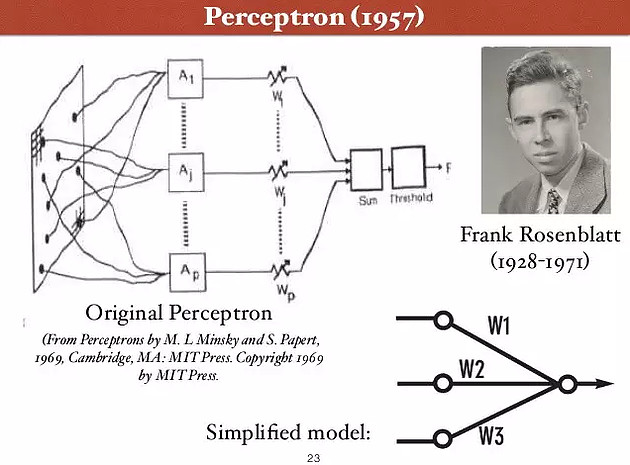
罗森布拉特给出感知机一个简单直观的学习方案:给定一个有输入输出实例的训练集,感知机「学习」一个函数:对每个例子,若感知机的输出值比实例低太多,则增加它的权重,否则若比实例高太多,则减少它的权重。该算法如下:
1、给权重系数置初值;
2、对于训练集中一个实例的输入值,计算感知机的输出值;
3、如若感知机的输出值和实例中默认正确的输出值不同:(1)若输出值应该为0但实际为1,减少输入值是1的例子的权重。(2)若输出值应该为1但实际为0,增加输入值是1的例子的权重;
4、对于训练集中下一个例子做同样的事,重复步骤2~3直到感知机不再出错为止。
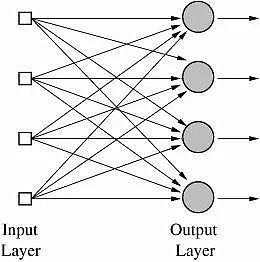
很重要的是,这种方法还可以用在多个输出值的函数中,或具有多个类别的分类任务。这对一台感知机来说是不可能完成的,因为它只有一个输出,但是,多输出函数能用位于同一层的多个感知机来学习,每个感知机接收到同一个输入,但分别负责函数的不同输出。
感知器是整个神经网络的基础,神经元通过响应函数确定输出,神经元之间通过权值进行传递信息, 权重的确定根据误差来进行调节,这就是学习的过程。这个方法的前提是整个网络是收敛的,1957年罗森布拉特证明了这个结论。

罗森布拉特在一台IBM-704计算机上模拟实现了“感知器”神经网络模型。感知器占据了整个实验室,它包括三层结构,运作机制并不复杂。感知器的一端,400个光传感器模拟视网膜;传感器多次连接一组512个电子触发器,当它通过一个特定的可调节的兴奋阀值时就会像神经元一样激发。这些触发器连接到最后一层,当一个物体与感知器受训见过的对象相互匹配时,它就会发出信号。这个模型可以完成一些简单的视觉处理任务。

康奈尔航天实验室的Mark I 感知机,第一台感知机的硬件
1958年夏,罗森布拉特和他的赞助方美国海军举行了新闻发布会。《纽约时报》当时报道说:“海军透露了一种电子计算机的雏形,它将能够走路、说话、看、写、自我复制并感知到自己的存在……据预测,不久以后,感知器将能够识别出人并叫出他们的名字,立即把演讲内容翻译成另一种语言并写下来。”

在美国纽约市水牛城的康奈尔航空实验室内,一名工作人员在调节罗森布拉特发明的人工神经网络中的电线和光线感应器(摄于1960年)
罗森布拉特1962年出版了一本书:《神经动力学原理:感知机和大脑机制的理论》(Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms),这本书总结了他的所有研究成果。
线性分类与异或问题
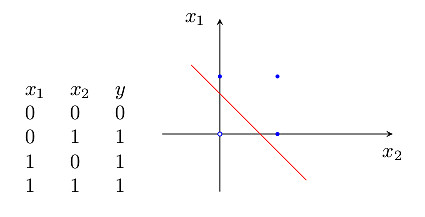
感知器简单而优雅,但它仅对线性问题具有分类能力。什么是线性问题呢?简单来讲,就是用一条直线可分的图形。比如,逻辑“与”和逻辑“或”就是线性问题,我们可以用一条直线来分隔0和1。
1)逻辑“与”的真值表和二维样本图:

2)逻辑“或”的真值表和二维样本图:
为什么感知器可以解决线性问题呢?这是由它的权重求和公式决定的。这里以两个输入分量 x1 和 x2 组成的二维空间为例,此时神经元的输出为
o=1,ω1x1+ω2x2−T>0/-1,ω1x1+ω2x2−T<0
所以,方程 ω1x1+ω2x2−T=0确定的直线就是二维输入样本空间上的一条分界线。在三维及更高维数的输入样本空间中,ω1x1+ω2x2+...ωnxn−T=0同样表征一个超平面可以划分样本空间。

但是如果要让它来处理非线性的问题,感知器就无能为力了。例如“异或”(XOR,两个输入如果相同,输出为0;两个输入如果是不同,输出为1),就无法用一条直线来分割开来,因此感知器就没办法实现“异或”的功能。
1969 年,马文·明斯基(Marvin Minsky)和西蒙·派珀特(Seymour Papert)出版了一本书《感知器:计算几何简介》(Perceptrons: An Introduction to Computational Geometry)。书中论证了感知器模型的两个关键问题:其一,单层的神经网络无法解决上面分析的不可线性分割的问题,典型例子如同或(XNOR,两个输入如果相同,输出为1;两个输入如果是不同,输出为0。)其二,受硬件水平的限制,当时的电脑完全没有能力完成神经网络模型所需要的超大的计算量。
异或问题的解决
首先我们再次建模神经元并用其实现与或非的逻辑功能:
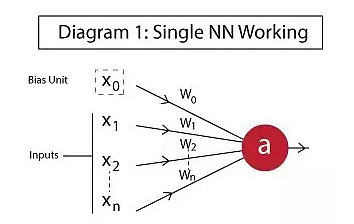
x1,x2,…, xN:神经元的输入。这些可以从输入层实际观测或者是一个隐藏层的中间值(隐藏层即介于输入与输出之间的所有节点组成的一层)。
X0:偏置单元。这是常值添加到响应函数的输入(类似数学里y=ax+b中使直线不过原点的常数b)。即截距项,通常有+1值。
w0,w1,w2,…,wN:对应每个输入的权重(偏置单元X0可以设置权重为1)。
a:神经元的输出。计算如下:
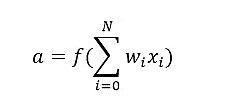
式子里的f是已知的响应函数,f使神经网络(单层乃至多层)非常灵活并且具有能估计复杂的非线性关系的能力。在简单情况下可以是一个高斯函数、逻辑函数、双曲线函数或者甚至是一个线性函数。现在我们利用神经网络实现三个基本逻辑功能:与、或、非(AND, OR, NOT)。
这里介绍一个基本的f函数,其实就是我们熟知的阶跃函数:
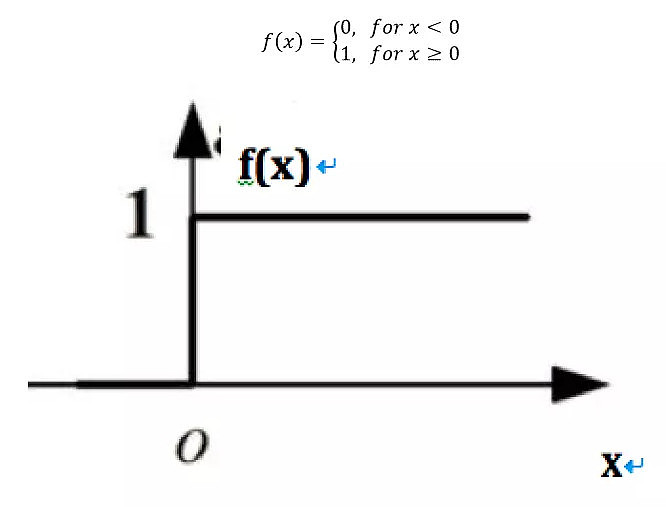
例1:and功能实现如下:
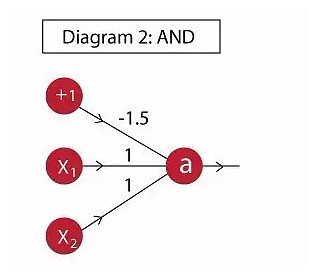
神经元输出:a = f( -1.5 + x1 + x2 )
真值表如下,可见列“a”与列“X1 AND X2”一致:

例2:or功能实现如下:
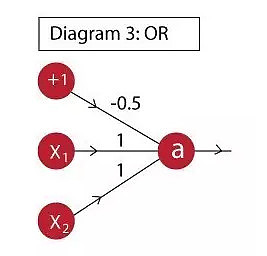
神经元输出为:
a = f(-0.5 + x1 + x2 )
真值表如下,其中列“a”与“X1 OR X2”一致:

通过例1和例2我们可以看到,只要改变偏置单元的权重,我们就可以实现or功能。如果x1或x2任何一个为正则权重总值为正。
例3:not功能实现如下:
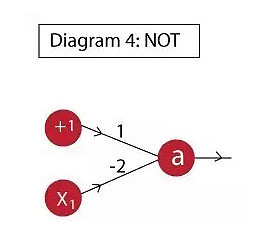
神经元输出为:a = f( 1 - 2 * x1 )
真值表如下:

之前我们看到的例子中与、或、非功能都是线性可分的,感知器只有输出层神经元进行响应函数处理,即只拥有一层功能神经元,学习能力非常有限。因此非线性可分要用到多层神经网络。
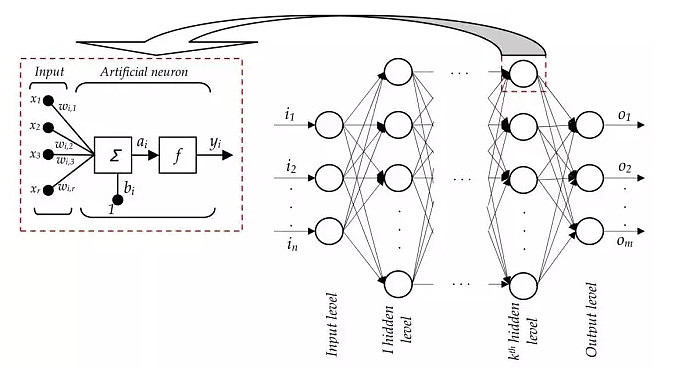
多层神经网络分为三种类型的层:
输入层:神经网络最左边的一层,通过这些神经元输入需要训练观察的样本。
隐藏层:介于输入与输出之间的所有节点组成的一层。帮助神经网络学习数据间的复杂关系。
输出层:由前两层得到神经网络最后一层。5个分类的情况下输出层将有5个神经元。
为什么多层网络是有用的?
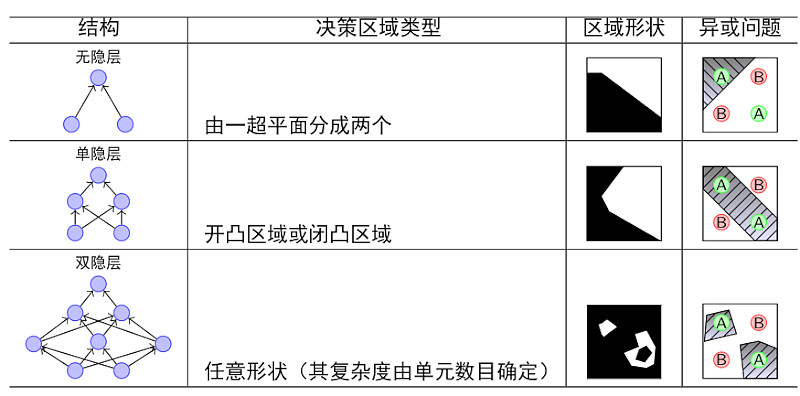
由上图可以看出,随着隐层层数的增多,凸域将可以形成任意的形状,因此可以解决任何复杂的分类问题。实际上,Kolmogorov理论指出:双隐层感知器就足以解决任何复杂的分类问题。
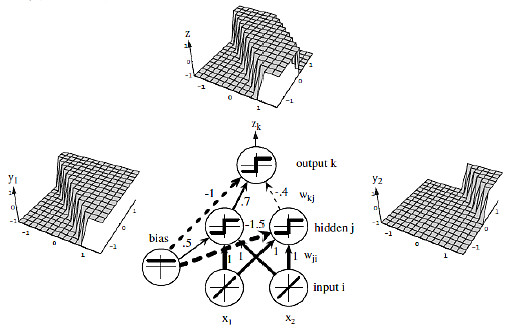
下面我们试着去了解神经网络如何用多层来模拟复杂关系。要进一步理解这个,需要举一个同或函数的例子。其真值表如下:
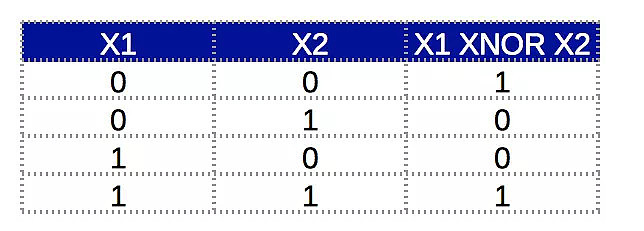
这里我们可以看到当输入都相同时,输出为1,否则为0。这种关系不能由一个神经元独立完成,因此需要一个多层网络。使用多层的背后思想是:复杂关系功能可以被分解为简单的功能及其组合。让我们分解同或函数:
X1 XNOR X2 = NOT ( X1 XOR X2 )
= NOT [(A+B).(A'+B') ]
= (A+B)'+ (A'+B')'
=(A'.B') + (A.B)
(注意: 这里符号“+”代表或 ,符号“.”代表与,符号“'”“-”代表非)
这样我们可以用之前讲解的简单的例子实现。
方法1: X1 XNOR X2 = (A’.B’) + (A.B)
设计神经元模拟A’.B’是一项挑战,可通过以下实现:
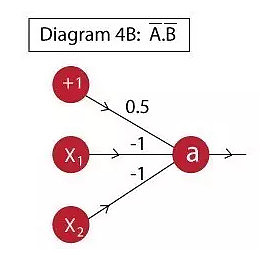
神经元输出:a = f( 0.5 – x1 – x2 )
真值表为:
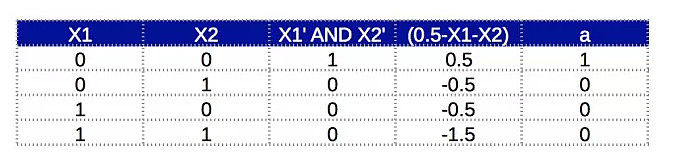
现在,可以分别把A’.B’和A.B当作两个独立的部分,并结合为多层网络。网络的语义图如下:
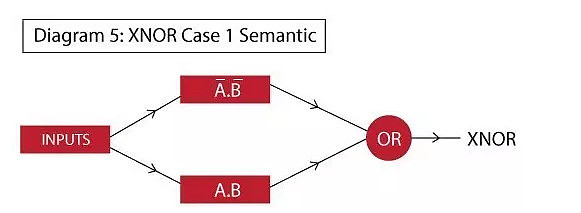
在这里可以看到,在第一层,我们分别确定A’.B’和A.B。在第二层,我们将输出并且在顶部实现OR功能。最后整体的网络实现如下图所示:
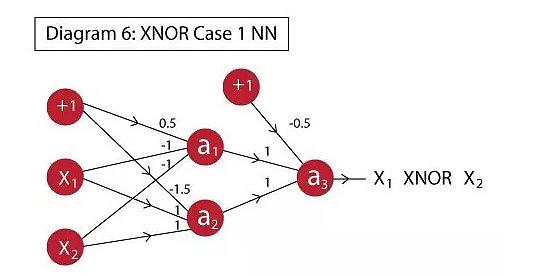
仔细看会发现这不过是我们之前画的神经元的组合:
a1:实现了A’.B’;
a2:实现了A.B;
a3:建立在a1和a2上实现OR,从而有效的实现(A’.B’ + A.B)。
通过真值表验证其功能:
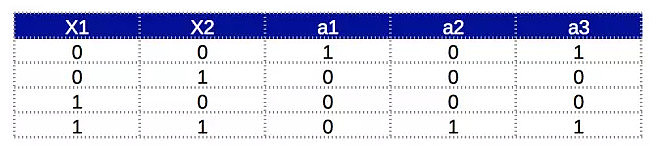
在上面的例子中,我们不得不分别计算A’.B’和A.B。如果我们想仅仅是基于基本的AND, OR, NOT函数实现同或功能的话,请看下面的方法2。
方法2: X1 XNOR X2 = NOT[ (A+B).(A’+B’) ]
这里我们用之前分解的第二步得到的式子来实现,网络的语义图如下:
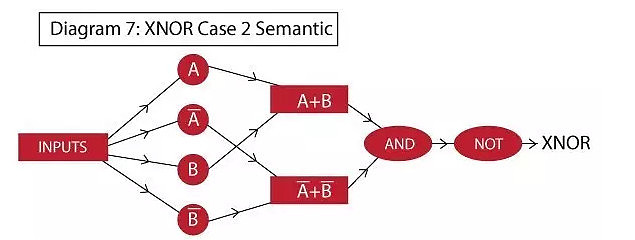
可以看到在这里神经网络不得不使用三个隐藏层。整体网络的实现和我们之前所做的相似:
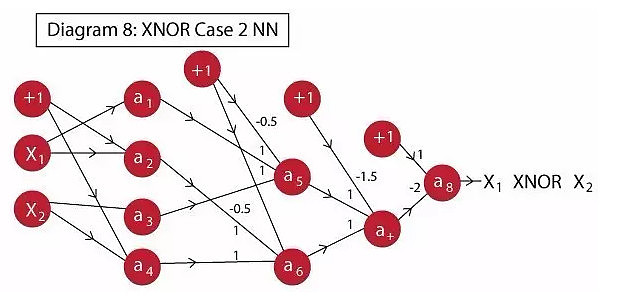
a1:等同于 A ;
a2:实现了 A’;
a3:等同于 B ;
a4:实现了 B’;
a5:实现了OR, 实际上是 A+B ;
a6:实现了OR, 实际上是 A’+B’;
a7:实现了AND, 实际上是(A+B).(A’+B’) ;
a8:实现了NOT, 实际上是 NOT [ (A+B).(A’+B’)],即最终XNOR的输出
真值表如下:


神经网络开启了人类对大脑的建模,推动了人工智能技术的发展,2004年IEEE Frank Rosenblatt Award成立,罗森布拉特被称为神经网络的创立者。