《统计学》读书笔记
 (2013-01-21 11:42:54)[编辑][删除]
(2013-01-21 11:42:54)[编辑][删除] 转载▼
转载▼ 标签: 杂谈 分类: 读书笔记
《统计学》,美David Freedman等著,魏宗舒等译,中国统计出版社出版。
第一部分 实验设计
第1章 对照试验
1. 一种新药的问世,怎样设计一个试验来测试它的效果呢?最基本的办法就是比较。把药分给处理组的病人,而把其他病人作为对照——他们不接受治疗。然后比较两个组的反应。病人将以随机的方式被 分到处理组和对照组,整个实验在双盲情况下进行。所谓双盲是说:不管是病人,还是测定反应的医生都不应知道谁在处理组谁在对照组。(老K:处理组和对照组 的分配一定要是随机的,以便排除其他因素的影响,从而让比较的结果反应药效而不是混杂其他原因。书中讲了实验时许多可能犯错的地方,事实上这些错误在我们 的投资分析中比比皆是,犯错后比较产生的结论自然不怎么可靠。)
2. 统计学家经常使用比较法。(老K:格雷厄姆在证券分析中使用了大量的比较法,或者说,格雷厄姆将统计学引入到了证券分析中。)
3. 在双盲实验中,实验对象不知道自己在处理组还是在对照组,那些评估反应的人也不知道这点。这样就防止了反应中或评估中的偏性。
第2章 观察研究
1. 对照试验不同于观察研究。在一个对照试验中,是研究者决定谁将在处理组和谁将在对照组。与此形成对照,在观察研究中,正是实验对象安排他们自己到不同的组 去,而研究者只是观察所发生的情况。比如:关于吸烟影响的研究必定是观察性的。......因此,在吸烟与疾病之间存在着一种强关联,但是这种关联并不等 同于因果关系。可能存在着某些隐蔽的混杂因素,它诱使人们吸烟——同时也使他们得病。之后,书中讲述了冠心病药物安妥明的试验,最后发现是“坚持”这个隐 蔽的性格因素使得更少的人死亡,而不是药物本身。还讲述了常发于贫穷地区的糙皮病的观察研究,人们一般认为是贫穷导致卫生差,苍蝇叮咬的关系,最后事实是 穷人们吃玉米,玉米里面的烟酸导致。苍蝇是贫穷的一种标志,而不是糙皮病的原因。相关联不等于因果关系。书中还讲述了研究生入学等其他案例。(老K:注意观察研究中的因果分析。)
第二部分 描述性统计
第3章 直方图
1. 直方图用面积而不是高度来表示数。由分布表开始绘制。(老K:跟我们常说的直方柱形图是有区别的。)
2. 为了计算小组区间上块形的高度,将百分数除以区间的长度。(老K:纵向刻度是密度,横向刻度是容积(比如年区间,或每千美元区间),块状面积是密度×容积=容量,即分布表的合计百分比。)
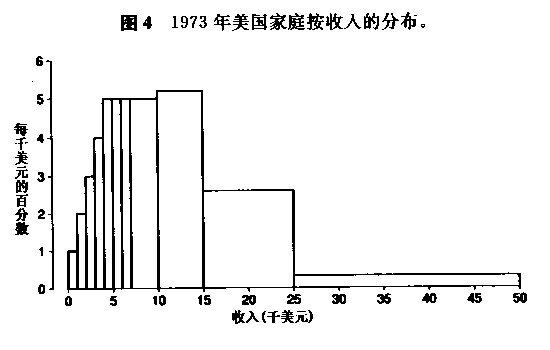
见上图。上图表示家庭收入在10000美元-15000美元的家庭占比约在5*5%=25%左右,这25%挤在这5千美元的区间里。而15000美元 -25000美元的家庭占比也约在10*2.5%=25%左右,这25%则分布在这1万美元的区间里,显得稍微宽敞些。所有块形面积加起来为100%。
而下图为某个拟做体重分布统计的直方图的草图,是错误的。因为其类似三角形,面积为1/2*100*4%=200%,错了。
3. 变量,是指研究中因研究对象不同而变化的一种特性。有些问题通过给出一个数而得到答案:对应的变量是定量的。有些问题是用修饰语来回答,对应的变量是定性的。定量变量可能是离散的或连续的,这不是一个严格而可靠的区分,但很管用。
4. 混杂因素有时候用交叉列表加以控制。
第4章 平均数和标准差
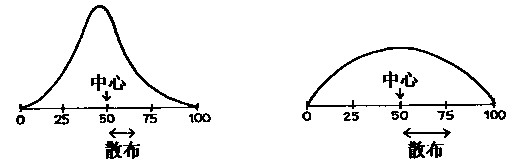
1. 平均数通常用来寻求中心,中位数也同样如此。标准差度量了关于平均数的散布程度,四分位数间距,则是散布的另一种测度。下图中,两者中心相同,但第2个直方图更分散一些。
2. 平均数。算术平均数是概括数据的一种强有力的方法。(老K:投资分析中,大多用到算数平均数就行了。格老常用。) 横向调查研究,纵向调查研究。(老K:即不同对象间同一时点的横向比较,同一对象不同时点的纵向比较。格老常用。)
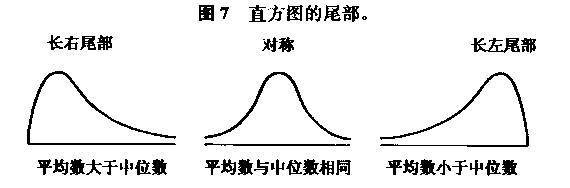
3. 平均数与中位数。直方图中,平均数左边的块形面积与右边的面积不一定相等。但在平均数处支撑,直方图保持平衡。(老K:想想跷跷板,两个不同重量的人坐在离中心不同距离的地方而保持平衡的样子。)直方图的中位数是这样一个数值,在它的左右两边各具有一半面积。参见下图:
4. 均方根,缩写为r.m.s.(root-mean-square)。
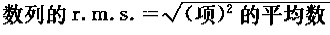
例:数列0,5,-8,7,-3。其平均数为0.2。r.m.s.约为5.4。
5. 标准差,简称SD。

标准差指出了数列中的数离它们的平均数有多远,数列中大多数项离开平均数大约1个SD左右,极少数项将离开2个或3个SD以上。一般来说,数列中68%(三分之二)的项在离平均数的1个SD范围内,其余的32%离得较远。95%的项在距平均数的2个SD范围内,其余的5%则远离之。这对许多数列是如此,但不是所有的数列都是这样。(老K:作为投资者,我们要特别关注尾部的风险和尾部的机会,即特别关注2个SD以外的部分。)
第5章 数据的正态近似
1. 正态曲线。1870年,一位数学家产生了一种想法,即将1720年由某人发现的正态曲线做为一种理想的直方图,使得数据直方图可以与之比较。(老K:所以 正态曲线只是大千世界众多直方图里面的一种而已。由于其特殊性,被用作比较基准。公式就不抄了,令人生畏,且我等不需要记住。)

曲线关于0点对称,曲线下面的总面积为100%。曲线在3和4之间变得非常低,但不接触。只有大约6/100000的面积在比-4小比4大的区间外面。每一项在平均数之上或之下多少个SD而被转换为横轴的标准单位。(老K:我猜长期资本管理公司应该就死于那6/100000的面积的风险概率之内。)
2. 正态曲线下,-1到+1之间的面积大约是68%。-2到+2之间的面积大约是95%。
3. 对于许多数列来说,在一个区间内的项的百分数可以估计如下。首先,将区间换算成标准单位;其次,求正态曲线下相应的面积;最后,将这2步合在一起。整个过程称为正态近似。近似在于求面积之前用正态曲线代替原来的直方图。(老K:目的就是求面积。可以用这个来估算事件概率吗?书中有句话:在本书的后面部分,我们将提出一类数学理论,它将有助于解释什么时候直方图会遵循正态曲线。)
4. 平均数和SD可以用来概括遵循正态曲线的数据。对于其他类型的数据,它们是不令人满意的。博文上面的美国家庭收入分布就是如此,它根本就不遵循正态曲线,它有一个长的右尾部,为了概括这样的直方图,统计学家常常使用百分位数。
5. 百分位数。收入分布第1百分位数指大约1%的家庭具有某个水平或更少的收入,第2百分位数指大约2%的家庭具有某个水平或更少的收入。这样,第50百分位 数就是中位数。四分位数间距等于(第75百分位数-第25百分位数),四分位数间距有时候用作散布的度量。所有直方图,不管遵不遵循正态曲线,都是可以用 百分位数来概括的。
第6章 测量误差
1. 如果同一样东西测量若干次,在理想的世界里每次将得到相同的结果。但在实践中是存在差异的。每一次结果都产生机会误差,误差随一次次的测量而变化。存在着 若干有关机会误差的问题:它们从哪里来的?可能有多大?在平均数中可能抵消掉多少?第一个问题是容易的:在大多数场合没有人知道(老K:哈哈,测不准原 理)。后面的问题后面解答。
2. 砝码NB10(国家标准局NB所拥有并且其名义上的值是10克——两个5美分镍币的重量),标准局每星期称一次,1962-1963年由Almer先生和 Jones夫人完成的100次称量中,尽一切努力使得每次测量遵循同样的程序、同样的环境、同样的气压温度等。数字大多数是这样 的:9.999600,9.999591,9.999601,反复的测量统计,发现误差平均数基本在400微克左右(1微克大概是一颗灰尘的重量)。如果 NB10的测量值从10克以下400微克跳到10克以上500微克,那么某些事情出了差错需要加以修整。
3. 不管多么小心地去做,得到的测量值可能有点不同于真值。如果重复一次,将显现一点不同。相差多少?在信赖任何一次测量值之前,必定要面对这个问题。回答的最佳办法是通过重复测量。
4. 离群点。上述测量结果拟合正态曲线不十分好。有一些较少的非凡事例。这样极端的测量值称为离群点。它们不是大错而造成的。(老K:但却正是这个混沌世界的 真实存在。)当研究者看到一个离群点时需要作出一个艰难的选择。要么省略它;要么不得不认可他们的测量值不遵循正态曲线。曲线的声誉如此之高使得第一种选择成为通常的一种选择——理论战胜了经验。(老K:人脑偏向于选择性地记忆线性的、对称的曲线,而不是那些混沌非线性的离群点。)
5. 偏性。屠夫每次称重时将拇指放在磅秤上,布店出售布匹时用布卷尺测量,该布卷尺已被日积月累地拉长。这不是机会误差——因为它总是偏向同一个方向。偏性以相同的方式影响所有测量值,将它们推向同一方向。机会误差随着不同次的测量而变化,有时向上,有时向下。单独测量值=精确值+偏度+机会误差。通常,仅仅观察测量值本身是没有什么办法察觉偏性的。
第7章 点和线的描绘
1. 笛卡尔坐标系。
2. 直线的斜率和截距。X坐标增加称为前移,Y坐标增加称为上升。斜率=上升/前移。截距是x=0时,y的值。
3. 直线的代数方程。y=mx+b,其斜率为m,截距为b。(老K:这一章的知识应该是初中时教的吧。)
第三部分 相关与回归
第8章 相关
1. 散点图。第二部分讨论的方法对一次处理一个变量是很有效的,而要研究两个变量之间的关系,则需要引入其他方法。下图表示了儿子身高和父亲身高关系的散点 图。每一个点,x表示父亲的身高,y表示儿子的身高。可见,日常生活中常说的较高的父亲有较高的儿子,这种相关性是多么的弱。如果你碰巧知道父亲的身高是 71.5英寸和72.5英寸之间(下图两条竖线之间),在试图预测他的儿子的身高中误差仍有大量余地。如果两个变量之间存在强相关,则已知一个变量的值对预测另一个变量的值将很有帮助。但若是弱相关,关于一个变量的信息对猜测另一个变量的值无多大帮助。

2. 社会科学研究中研究两个变量的关系时,常常把一个变量称为自变量,另一个变量称为因变量。通常认为是自变量影响因变量,而不是因变量影响自变量。然而,没有什么东西可以阻止研究者把儿子的身高作为自变量。
3. 相关系数。相关系数是线性相关或围绕直线群集程度的一种度量。两个变量之间的关系可用如下统计量进行概括:所有x值的平均数,所有x值的SD,所有y值的 平均数,所有y值的SD,相关系数r。r的计算稍后再讲。下图中,左图的散点更靠近直线,相关系数大一些,右图松散一点,相关系数小一些。如果全部在一条直线上,则通常称为完全相关。
4.弱相关是社会科学研究中的通例,r的值通常在0.3至0.7之间。(老K:看看上面的图就知道,一般来说,定性、眼光混合了那么多变量,最 终结论与变量的关系其实是多么的弱)。要注意的是:r=0.80并不意味着80%的点都紧密地群集在一条直线的周围,也不表示其线性程度是r=0.40情 况时的两倍。
5. 负相关。不用多解释,看下图就明白了(相关系数为-0.70)。相关系数总是在-1和1之间的。

6. SD线。当r越接近1时,点将越密集地群集在一条直线旁。这条直线称为SD线。该直线的斜率为:正相关:(y的SD)/(x的SD);负相关:-(y的SD)/(x的SD)。
7. 计算相关系数:将每个变量都转换为标准单位,乘积的平均数即为相关系数。r=[(以标准单位表示的x)*(以标准单位表示的y)]的平均数。(老K:具体计算示例过程和为什么r能度量相关程度的原因,不抄了,我不用考试哈)
第9章 再谈相关
1. 相关系数的特点:首先,相关系数是一个数,变量的所有值都乘以同一个正数或增加同一个数,r都不受影响。第二,x与y之间的相关系数等于y与x之间的相关系数。
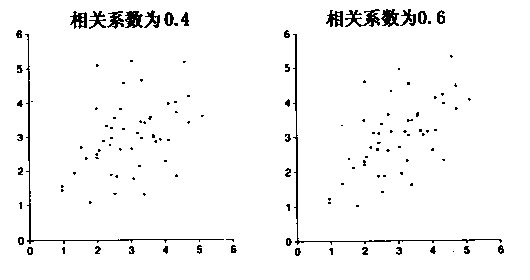
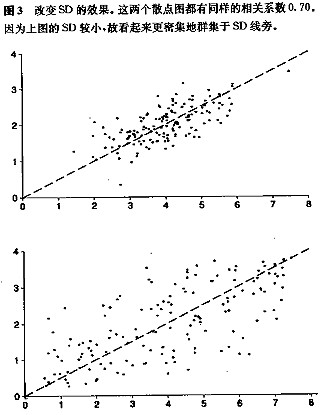
2. 散点图的形状依赖于SD。r不是按绝对值度量群集程度,而是按相对值——相对于SD。下面2个图具有相同的相关系数0.70。
3.有时候用相关系数来描述散点图是一种很糟糕的办法。离群点和非线性就是两个成问题的情况。只要可能,应通过观察散点图检查离群点和非线性相关:r测量的是线性相关,不是一般意义上的相关。(老K:这段话很重要。因为投资世界分析非线性居多,离群点需特别关注。)
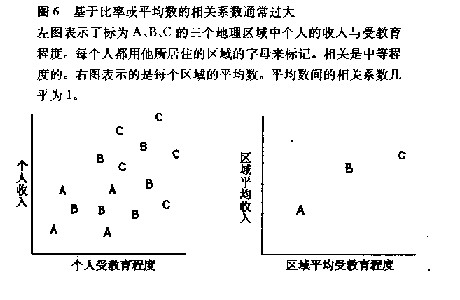
4. 生态相关。1955年,Doll发表了一篇划时代的文章,论述了吸烟与肺癌之间的关系。其论据之一是在是一个国家中吸烟率(按人计算)与肺癌死亡率之间关 系的散点图。对个人而不是国家的测量也是有效的,倾向于支持Doll的观点。但是,基于比率或平均数的相关系数常使人误入歧途。有个例子:美国人口 25~64岁男子的收入与受教育程度之间的相关系数4约为0.4。但把美国分为9个区域,计算出每个区域的男子平均收入和平均受教育陈鼓,发现两者相关系 数为0.7。如果你用区域的相关系数来估计个人的相关的系数,你将大错特错。原因如下图所示。生态相关是基于比率或平均数的。它们通常用于政治科学和社会学领域。它们倾向于夸大相关程度,因此要小心一些。
5.相关不是因果关系。相关系数度量的是相互关系,但相互关系并不等于因果关系。(老K:这个论点前面2章有提及。书中举例分析了受教育程度和失业、物种生存范围与生存期间、饮食中的脂肪与癌症之间的关系,分析过程非常保守,即使存在一定程度的相关,也不能确认因果。)
第10章 回归
1. 回归线。跟散点图聚集的SD线不同。y关于x的回归线估计了相应于每一个x值的y的平均数。用相关系数估计每个x值所对应的y的平均数的方法叫回归方法。 这种方法可叙述如下:x每增加1个SD,平均而言,相应的y增加r个SD。下图中,虚线为SD线,实线为回归线,相关系数r为0.47。(老K:这个有点 复杂了,回归线能派什么实际用场呢?)

2. 平均数图。表示了每一身高下,该人群的平均体重。回归线是平均数图的光滑形式。如果平均数图正好是一条直线,则回归线和平均数图必然合为同一条直线。
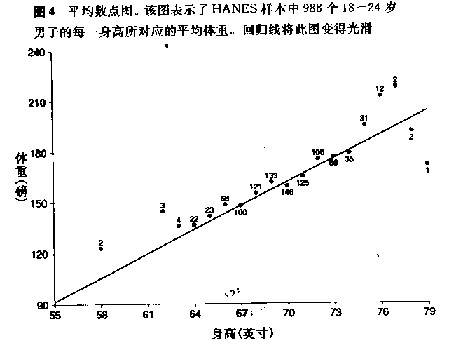
3. 用于个体的回归方法。一般规则是:当你需要从另一个变量预测一个变量时,采用平均数。在许多情况,回归方法给出了估计新平均数的合理实用的方法。当然,如果变量之间存在非线性关系,则回归方法不适用。
4. 回归谬论。学前班入学前考试一次,入学后考试一次,两种情况下分数接近,似乎没什么效果。但发现学前测试中低于平均数的儿童在学后测试中平均提高了5个智 商点,与此相反,在学前测试中高于平均数的儿童,在学后测试中平均降低了5个智商点。这就是回归效应。回归谬论认为回归效应是由于某些重要因素引起,而不 仅是围绕直线的散布所致。书中又举了矮爸爸高儿子和高儿子矮爸爸的例子。最终建立了一个学前考试-学后考试的模型:考试的观察分数=真实分数+机会误差。对于考高分的人,更可能的解释是产生了正的机会误差,对于考低分的人,更可能的解释是产生了负的机会误差。(老K:这个有点意思。另,书中说丈夫和妻子智商之间的相关系数为0.50,呵呵,平时要夸夸LP聪明啊)
第11章 回归的均方根误差
第12章 回归直线
(老K:这两章太学究,恐怕带沟里,跳过。)
第四部分 概率
第13章 机会是什么?
1. 本书将介绍频数论,这一理论对可以在同一条件下独立地多次重复的过程最能奏效。机会游戏属于这一范畴,事实上,许多频数理论是为了解赌博问题而得到发展的。Adraham de Moivre是这一理论的最伟大的大师之一。他的著作《机会论》的部分献刊词印于下:“......由经验知道,对掌握推理艺术来说,没有什么能比对从无可置疑的原则出发,正确演绎出来的一长串推断进行思考更有助益,对此本书提供了大量例子。”(老K:注意了,这种概率思维只对于在同一条件下能独立地多次重复的过程有效,比如抛硬币等。对于特定时间的某次特定稀有事件,很难证明此种思维有效。本章最后的Collins案件又提到了这一点。这个很容易被忽视。)
2. 当某一基本过程在相同条件下独立地一次又一次进行时,某事件的机会给出了期望该事件发生次数的百分数。机会是在0%与100%之间。某事件的机会等于 100%减去其对立事物的机会。如果一个事件有3次机会发生和2次机会不发生,分数3/5将恰当地表示这一事件发生的概率,并且可以取作这一概率的度量。 (老K:这章东西太简单了,不过还是抄在这里吧。大学时俺曾是《概率》课程的班级课代表,期末考试99分远高于班级平均分,现在大概99%都还给老师了, 呵呵。)
3. 条件概率。一副牌52张洗过后,取最上面2张牌铺在桌上,问第2张牌是红心Q的机会是多少?翻开第一张牌是梅花7,第2张牌是红心Q的机会是多少?(答案:1/52,1/52)。1/51称为条件机会,1/52称为无条件机会。
4. 乘数法则。通过概率相乘去计算两个事件发生的机会。一个盒子红白蓝3张票,先抽出红色票,再抽出白色票的机会是多少。(1/3×1/2=1/6)。两件事情一起发生的机会等于第一件事情发生的机会乘以已知第一件事情发生的情况下第二件事情发生的机会。
5. 独立性。如果给定第一件事,无论它的结果是什么,第二件事情的机会都一样,称两件事情是独立的。否则,他们是不独立的。某人抛一枚硬币两次,如果第二次抛 得头像,你赢1美元。(a)假如第1次抛得头像,你赢1美元的机会是多少?(b)假如第1次抛得背面,你赢1美元的机会是多少?(c)这2次抛硬币独立 吗?(50%,独立的)。随机并放回地抽取时,各次抽取是独立的。不放回抽取时,各次抽取是不独立的。如果两个事件是独立的,那么这两个事件都发生的机会等于它们各自无条件概率的乘积。(老K:最后一句话也许能对定性思维稍微提个醒。另外,事件的独立性在现实世界里有时难以推断。)
第14章 再谈机会
1. ...一本教会人们把真理和看起来非常接近真理的事物区分开来的这类书,可视为适当推理的帮手。——Abraham De Moivre
2. 列举状态法。3颗骰子掷出点数和为9与掷出点数和为10的机会各为多少?和为9有6种组合:126,135,144,234,225,333,和为10也 有6种组合:145,136,226,235,244,334。赌徒们以为9和10机会相同,但实际上10的机会稍多一点。伽利略帮助解决了这一问题。将 3颗骰子染成不同颜色,并列出所有状态,发现对9来说,333只有一种排列,而对10来说,334这组实际上意味着3种排列。所以,掷出9的机会是 25/216,掷出10的机会是27/216。
3. 加法规则。如果一件事情发生制止了另一件事情的发生,则两件事情是互不相容的。为求两件事情中至少有件发生的机会,检查一下它们是否互不相容,如果是的,把它们的机会相加。
4. 某人掷一对骰子,正确还是错误:至少得到一个幺点的机会是1/6+1/6=1/3。(错误,不是互不相容的。多计算了两个骰子都是幺点的机会。正确答案是(6+6-1)/36=11/36。)(老K:相加相乘时要小心。)
5. Chevalier de Mere悖论。掷一个骰子4次,至少出现一个幺点的机会,与掷一对骰子24次,至少得到一对幺点的机会是否相等。赌徒们的计算是4×1/6=2 /3,24×1/36=2/3,所以是相等的。实际上却不是这样。这里相加出现了问题,因为两次事件并非互不相容。那应该如何计算呢?计算其相反的情况。 掷一个骰子4次,不出现任何幺点的机会是(5/6)的4次方,即48.2%,所以掷一个骰子4次,至少出现一个幺点的机会是100%- 48.2%=51.8%.而掷一对骰子24次,不出现任何幺点的机会是(35/36)的24次方,即50.9%,所以掷一对骰子24次,至少出现一对幺点 的机会是100-50.9%=49.1%。51.8%>49.1%,两者机会不等。(老K:相加只在互不相容时使用,相乘只在独立时使用。切记。)
第15章 二项系数
1. 一个盒子装有1颗红弹子和9颗绿弹子。随机放回地抽取5次,恰好有2次取得红弹子的机会是多少?(先看有几种排列可能,RRGGG是一种,然后再看这种可 能的概率是多少。每一种的机会是(1/10)*(1/10)*(9/10)*(9/10)*(9/10),一共有几种可能(2个R,3个G)呢?这种可能 的排列个数称为二项系数,公式:5*4*3*2*1/((2*1)*(3*2*1))=10种。所以恰好得到2次红弹子的机会是10*((1/10)* (1/10)*(9/10)*(9/10)*(9/10)),约为7%)
2. 二项系数用数的右边放一个惊叹号表示。惊叹号读作阶乘。如4!=4*3*2*1=24。“4的阶乘等于24。”0!约定为1。之前的例子,排列可能为5!/(2!*3!)。把10个R和10个G拍成一行的可能方式有20!/(10!*10!)种。
第五部分 机会变异
第16章 平均数律
1. (书中以虚拟对话的方式讲述一个常人不大在意的错觉。抛硬币10000次,大家预计5000次是头,5000次是字,但实际上出现了5067次头。如果你 觉得再抛10000次,可能就会多出现字,那就错了。因为每次抛硬币前,概率是独立的,都是1/2,并不能指望其来回反复。人们的期望值为5000,但头 像数=抛的次数的一半+机会误差。如果再抛10000次,机会误差的绝对值可能继续增大,但是增加值占抛的次数的百分比会下降,约为所抛次数的平方根。)
2.对于由机会过程产生的数,存在机会变异,尽量将其与从一只盒子中抽得数之和(比如:一只盒子放有123456六个数,随机放回地抽取25次,观察到值 在75和100中反复,那么所得和在75与100之间的机会是多少呢?)中的机会变异之间建立联系。比如Nevada轮盘赌,0和00是绿色,1-36红 黑相间。赌黑,相当于一个盒子里面放有38张票,其中18张票子上写+1,20张票子上写-1,每次下注相当于从盒子里面随机放回地抽取一张票子,多次下 注则将票子上的数字相加,就是亏(赢)。
第17章 期望值与标准误差
1. 期望值。正在进行一个机会过程,它报出一个数,随后另一个数,再另一个数,你几乎将被淹没在随机输出之中,但是数学家在这种紊乱中发现了一些规律:这过程 给出的数围绕着期望值变化,其偏离量的大小与标准差相似。随机放回地从盒中抽取所得数之和的期望值=(抽取次数)×(盒平均)。
2. 标准误差。一个盒子有023456六个数,假设从盒子中随机放回抽取25次,其和的期望值为5×0+5×2+5×3+5×4+5×5+5×6=75。实际 抽取时的和=期望值+机会误差。机会误差可能有多大?答案由标准误差(简写为SE)给出。一个和可能在它的期望值附近,但是偏离一个其大小与标准误差相似 的机会误差。标准误差是抽取次数的平方根乘以盒子的SD。(老K:SD是标准差,上文有讲述。)SD和SE是不同的,SD适用于一系列数字的散布程度,对 比之下,SE适用于机会变异——例如抽取所得数之和中的机会变异(老K:比如赌博)。
3. 正态曲线。后文用正态曲线模拟了随机抽取数之和。(老K:略,常进赌场的赌徒们看完这些,应该知道他们挑战的是曲线尾部的部分。)
4. 平方根法则是平均数律的数学解释。(见上一章的1)
5. 附言:赌得愈多,输得越多。轮盘赌、掷骰子及其他类似的不公正赌博中,没办法调整你的盈利期望值为正。这是一个数学定理。但是,二十一点的赌博是个 例外,在这种赌博中某些情况下存在一些具有正期望值盈利的打赌。其结果是,人们在二十一点赌博中赢得过许多钱。(老K:有空研究研究二十一点,网上搜了 下,好像赌场也改进了,呵呵。投资就是要做期望值为正的赌博哈。)
第18章 概率直方图的正态近似
1. 概率直方图,用面积表示机会,而不是表示数据。
2. 抛100次硬币,正好出现50次头像的概率约为8%。随着抛的次数增加,一个硬币出现头像次数的概率也越来越接近正态曲线。抛900次,概率直方图已经和 正态曲线没有区别。从盒子中抽取数字,和的概率直方图随着抽取次数增加,也近似正态曲线。(老K:投资现实中,估算概率没有抛硬币,抽数字这么简单。)
第六部分 抽样
第19章 抽样调查
1. 研究整个总体一般并不实际,能检测的只是它的一部分,这部分称为样本。调查人员将根据部分对整体做出归纳,更为专业的措辞是,他们根据样本对总体做出推断。
2. 通常存在着调查人员需要知道的关于总体的某些数值特征,这些数值特征称为参数。参数由统计量或可根据样本算得的某些数值进行估计。只有当样本代表了总体时,根据样本估计参数才合理。有些选取样本的方法效果较差,有的很可能提供有代表性的样本。本章的两个主要课目是:选取样本的方法至关重要;最好的方法包含有计划地引用机会(概率)。
3. 抽样程序将这一类或那一类人排除在样本之外所表现出的系统倾向称为选择偏性。当选择程序有偏性时,抽取一个大的样本并无帮助。它只不过是在 较大的规模下去重复基本错误。(老K:有些统计上市公司行业长期回报率的报告,草率地称某一两个行业长期回报率显著高于其他行业,就很有可能犯了选择偏性 的错误。比较时,那些中途退市的、重组的、未上市的都没被选择在内。)
4. 调查时,有人回答,有人不回答。不回答者可能非常有别于回答者,当出现高不回答率时,谨防不回答偏倚。
5. 在定额抽样中,样本被精心挑选以使在某些关键特征上与总体相似。这方法似乎合理,但并不怎么奏效。原因是无意的偏倚。
6. 简单随机抽取意即随机不放回地抽取(盒子中的数字),与定额抽样相比较,这将产生好得多的结果,但在选举调查时,抽取简单随机样本不实际,因此,绝大多数调查机构采用多阶分群抽样的方案(按地域划分群、再划分选区、分区...)。
7. 简单随机抽样是基本的概率方法(2个重要特征:访问员对访问谁毫无决定权;选样本有明确的程序,且包含概率的有计划使用)。定额抽样不是一种概率方法,访问员在选择访问对象上有太多决定权。
8. 盖洛普民意测验在1948年时使用的样本容量约为50000人,误差约为5%。现在使用1/5到1/10的样本,但采取概率方法后,精度明显提高,已经能 以惊人的精度预测选举结果。(即使选取样本时用的是概率方法,某种程度的偏性几乎是不可避免的。如:不投票者、未决定者、回答偏性、不回答偏性、家庭偏 性...)
9.概率抽样下,使必然性变为可能性。而判断方法选择往往带有偏性,而机会(概率)是不带偏性的。这就是概率方法比判断方法奏效的原因。为极小化偏性,就应该使用不带偏袒性且客观的概率方法选取样本。
第20章 抽样中的机会误差
1. 随机抽样中,样本中男性的比例并不会与整体中男性的比例相等,会由于机会误差而偏离。机会误差有多大呢?答案由标准误差给出。(计算过程略)
2. 新墨西哥州的民意调查样本是从500选民中选1名,而得克萨斯州的民意调查是从5000选民中选1名,似乎新墨西哥州的民意调查比得克萨斯州的民意调查精 确。但是这是直觉与统计理论正面冲突的地方之一,而且必须让步的正是直觉。事实上,从新墨西哥州所能期望的精度与从得克萨斯州所能期望的精度几乎相同。当 估计百分数时决定精度的是样本的绝对容量,而不是相应总体的大小,这在样本仅为总体的一小部分的通常情况下也是正确的。(老K:所以,采取分析历史数据的方法对某个企业做推断,历史数据越充分越好。)
3. 盖洛普民意测验中二亿选民中抽取几千人就以令人满意的精度预测选举的结果,这怎么成为可能的呢?......对于2500选民的样本,机会误差的可能大小仅为1%左右。
第21章 百分数的准确性
(存在一些按标准误差计算的机会误差,投资决策不需要如此精确的概率,掠过,仅对出现的一个名词“置信区间”记录一下。)
1. 置信区间。总体的百分数置信水平约为95%的置信区间,意思是说:25000名注册学生,抽取了一个400名学生都简单随机样本,结果是317名住在家 里。估计那学期住在家里的学生数百分比。样本百分数为79%,标准误差为2%,4%的标准误差代表2个SE,2个SE代表95%的置信区间:你可能有 95%的把握住区间75%到83%内逮住总体的百分数。3个SE代表99.7%的置信区间:你可能有99.7%的把握在区间73%到85%内逮住总体的百 分数。...没有SE的倍数能给出100%的把握,因为总存在极小的可能性会出现非常大的机会误差。数学上这一点由正态曲线没有限定的范围这一事实所反 映。(老K:芒格曾说,统计学记住那个钟型曲线(正态曲线)就行了,也曾说,他们的一些洞察力来自统计学。)
第22章 估量就业与失业
(详细描述了统计局统计失业率的复杂过程,略。显然这些官方统计值与实际情况比较,也是存在误差和潜在偏性的。)
第23章 平均数的精度
1. 当从盒子中随机抽取时,抽得的平均数的概率直方图将遵循正态曲线,即使盒子里的数值并不如此。直方图必须换算成标准单位,且抽取的次数必须充分大。
2. (根据样本平均数,依置信区间反推总体平均数,误差为置信区间代表的方差SE。略。)
第七部分 机会模型
第24章 测量误差模型
1. 第6章NB10的测量。“confidence”(置信)一词在这儿是作为一个提示,提醒我们机会存在于测量过程而不是在被测量的事物中:确切重量不受机 会变异的支配。机会存在于测量过程中,而不是在被测量的事物中。只有当拥有相当多的测量值时,才用正态曲线来获取置信区间。
2. 将标准误差赋予重复测量的平均数,只有当数据的变异性与从盒子中重复抽取的变异性相似时方法才是合理的。如果整个期间数据呈现一定趋势或规律模式,盒子模 型不能应用,平方根法则只适用于取自盒子中的抽得数。比如1790-1980年,美国人口持续稳定地上升。(老K:盒子模型比较适合于围绕某个中心平衡值 上下波动的情况,不管这个中心平衡值是和还是平均值,于投资领域,我马上能想到的是社会平均利润率、通胀率于某一个平均值下的变化。)
3. 测量时,测量值=确切值+偏度+机会误差。NB10的测量中,我们不考虑偏性。在其他场合,偏性可能比机会误差更严重——而且更难发觉。(老K:在投资分析中,偏性比比皆是,也不大可能被杜绝。)
4. 统计推断能够通过对数据提出一个明确的机会模型而证明其合理性。没有盒子,就没有推断。(老K:数据对象不类似于盒子模型,就不能推断。)
第25章 遗传学中的机会模型
1. Mendel遗传学理论很伟大。(老K:类似X/Y染色体配对的事情。)
2. 但是根据其实验提交的数据来看,其机会误差太小,不符合总体随机模型。所以有可能Mendel的数据是经过加工的,可能是其园艺助手。
3. 遗传学是很好的应用机会模型的领域。(老K:巴菲特曾说抽中了卵巢彩票,生在美国。)
第八部分 显著性检验
第26章 显著性检验
1. Z=(观察值-期望值)/SE。Z表明一个观察值与它的期望值相差有多少个SE。期望值总是从原假设出发计算出来的。如,一个样本的平均数低于期望值3倍或3倍以上的SE,Z=-3,查正态曲线面积可知,这样的机会大约只有千分之一。这类机会称为一个观察到的显著性水平。
2. 观察到的显著性水平是得到一个与观察值同样极端或更极端检验统计量的机会。机会是在原假设为真的基础上计算出来的。机会越小,反对原假设的证券越强。(老 K:看起来不像是真的,往往就不是真的。用原假设来计算显著性水平,并依显著性水平来反对原假设,好像有点类似投资分析里面的质疑过程。科学就是证伪的过 程?)
第27章 再论平均数检验
第28章 X平方检验
第29章 显著性检验的更准确的考虑
(略,后3章没怎么看了,都是评估统计数据是否接近总体情况的方法)
(老K:基本上认同芒格所说的统计学主要记住那个正态曲线就行了的观点。其他的就是拿SE算来算去,看看统计结果与事实有多接近。科学就是不断地观察、假 想、立论,并不停地证伪,试图尽量接近真实情况,看多了书,觉得好多领域都一样,物理、天文、经济、投资、社会等等。2013.2.22)
(完)